A.Yajima and S.Machida
Graduate School of Science, Kyoto University, Kyoto 606-01, JAPAN
E-mail: yajima@kugi.kyoto-u.ac.jp
Numbers of numerical simulations of auroral particle acceleration process
have been performed in the last 20 years. Auroral particles are thought
to be accelerated along the magnetic field line by many small electrostatic
potential drops, called ``weak double layers", which are distributed
along the magnetic field line in the auroral zone. The field-aligned current
excites the electrostatic ion-acoustic waves, and the weak double layers
are formed as a result of nonlinear development of the ion-acoustic waves.
Thus, particle electrostatic codes are suitably adopted in studying such
an instability due to velocity space nonequilibrium. Those simulations are
usually one-dimensional, since it has an advantage that we can put many
grids along the magnetic field line and many particles in each grid.
A potential drop of the weak double layer was observed with a localized
density depletion in the background plasma ions. This fact is consistent
with simulation results that the weak double layer is an ion hole in the
ion phase space. The growth and movement of ion holes are synchronized with
the behavior of weak double layers [Barnes, 1985; Tetreault, 1991]. Ion
holes were formed in the stationary ion, but the upflowing ion is usually
observed in the auroral acceleration region [Koskinen,1990]. Effects of
this component must be studied. Gray et al.[1991] studied this hot
upflowing ion by numerical simulation, but electrons were stationary which
did not compose the field-aligned current. In our study, upward field-aligned
current consists of both shifted Maxwellian electrons and upflowing ions.
We performed two types of numerical simulation, two component model and three component models. Both of simulations were studied with aperiodic one dimensional electrostatic particle code.
The two component model includes hot shifted Maxwellian electron which carries upward field-aligned current, and stationary cold ion. We set the value of ion to electron temperature ratio as well as the electron drift velocity to cause the ion acoustic instability.
The difference between this model and aforementioned ``two component" model is the presence of an upflowing ion beam component. A field-aligned upflowing ion beam is commonly observed in the auroral particle acceleration region by satellite, but the existence of such a component was not taken into account in the two component model. In the three component model, we assumed hot electrons, cold ions, and hot ions which represent upflowing ion of our initial conditions.
The plasma parameters for our simulation are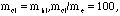 
in two component model 
in three component model 
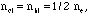and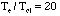 
.
Other simulation parameters are: (system length)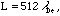 
(spatial grid)
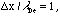(time
step)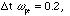 
and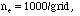 
where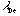
is the Debye length and 
is the electron plasma frequency.
We present four cases of simulation, run1 is the two component model, run2,
run3 and run4 are the three component model. Fig.1
shows parameters and initial velocity distribution function for those four
cases.
In our model, the system was set to be charge neutral, and both boundaries
have equal values of electric field. We fixed this value to be zero, because
it is necessary for simulation system to have net electrostatic potential
drop between both boundaries. Particle boundary condition is a modified
periodic condition. Particles out of one boundary are reinjected into the
simulation system from the other boundary with shifted-Maxwellian velocity
distribution. Drift velocity of each component is calculated by averaging
velocity of the particles in one grid at the boundary. Using this boundary
condition, one boundary does not affect the other boundary even if the region
near the boundary contains beam-like accelerated particles.
Many weak double layers were formed and vanished successively in the two component model. This process was also observable as an ion hole movement in the ion phase space. Ion hole was formed at the same velocity of the ion sound speed initially, then it was accelerated by potential drop owing to the charge layer around ion hole. Subsequently, ion hole left across cold ion in ion phase space in accordance with the disappearance of the potential drop. Ion acoustic solitary wave forming this weak double layer propagates downward and construct next weak double layer. Total potential drop was maintained by repetition of such a process. We call the weak double layer formed in this case type1 weak double layer.
As seen in the previous model, many weak double layers were formed and vanished
successively in the three component model as well. However, a major difference
between the two models is the life time of an ion hole, that is, the ion
hole existed longer in this system where the ion beam was assumed than in
a system where it was absent.
A important difference from run1 and run2 is the simultaneous existence
of other type of weak double layer. Ion hole was formed at the same velocity
of the ion sound speed of hot ion slow mode initially. We call this type
of weak double layer having upward velocity initially type2 weak double
layer.
The results of this model indicate that a theory of weak double layer formation
incorporating the ion hole as demonstrated in the former model is also applicable
to this model. Consequently, the total potential drop can grow in the present
model more than in the previous model.
Fig.2 shows movement of two types of weak double
layer in ion phase space.
Type1 weak double layer causes an acceleration of ion beam, and the ion
acoustic wave of slow beam mode is excited, followed by formation of type2
weak double layer. A single weak double layer can act positively to produce
more weak double layers in higher altitudes through the effect of ion beam.
Fig.3 shows such process schematically.
Gray, P. C., M. K. Hudson, W. Lotko, and R. Bergmann,
Decay of Ion Beam Driven Acoustic Waves into Ion Holes,
Geophys. Res. Lett., 18,1675,1991
Koskinen, H. E. J., R. Lundin, and B. Holdback,
On the plasma environment of solitary waves and weak double layers,
J. Geophys. Res., 95,5921,1990
Tetreault, D. J.,
Theory of electric fields in the auroral acceleration region,
J. Geophys. Res., 96,3549,1991
